题目内容
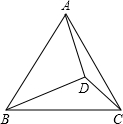 如图,D为正三角形ABC内一点,BD=5,CD=3,∠ADC=150°,则AD的长为
如图,D为正三角形ABC内一点,BD=5,CD=3,∠ADC=150°,则AD的长为4
4
.分析:如图,把△BDC绕D逆时针旋转60°到达△AEC,连接DE,根据旋转的性质和勾股定理,即可求出AD的长.
解答:解:把△BDC绕C逆时针旋转60°到达△AEC.
则△DCE为正三角形,DE=3,AE=BD=5,∵∠ADE=150°-60°=90°,
∴AD=
=4.
故答案为4.

则△DCE为正三角形,DE=3,AE=BD=5,∵∠ADE=150°-60°=90°,
∴AD=
| AE 2-DE 2 |
故答案为4.
点评:本题考查了等腰直角三角形的性质、全等三角形的判定和性质以及旋转的性质,①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 5、如图,P为正三角形ABC外接圆上一点,则∠APB=( )
5、如图,P为正三角形ABC外接圆上一点,则∠APB=( )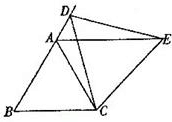 23、如图,△ABC为正三角形,D为边BA延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.
23、如图,△ABC为正三角形,D为边BA延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.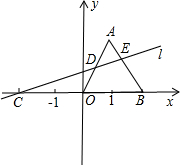 如图,△AOB为正三角形,点B坐标为(2,0),过点C(-2,0)作直线L交AO于D,交AB于E,且使△ADE和△DCO的面积相等,求直线L的函数解析式.
如图,△AOB为正三角形,点B坐标为(2,0),过点C(-2,0)作直线L交AO于D,交AB于E,且使△ADE和△DCO的面积相等,求直线L的函数解析式.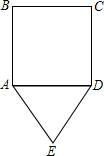 如图,△ADE为正三角形,四边形ABCD为正方形,AD=
如图,△ADE为正三角形,四边形ABCD为正方形,AD= 如图,D为正三角形ABC外接圆上的一点,则图中等于60°的角共有
如图,D为正三角形ABC外接圆上的一点,则图中等于60°的角共有