题目内容
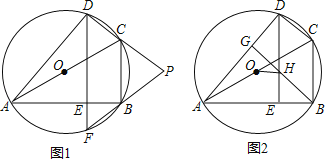
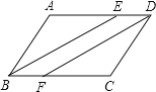
【题目】如图,在平行四边形ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.
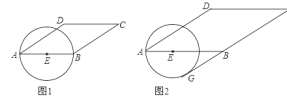
(1)如图1,若E是AB的中点,求⊙E在AD所在的直线上截得的弦长;
(2)如图2,若⊙E与BC所在的直线相切,求AE的长.
【答案】(1)AF=8;(2)AE=![]() .
.
【解析】
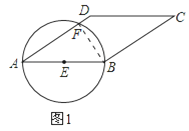
(1)设AD和圆相交于F,连接BF,由圆周角定理可得BF⊥AD,所以BF=8,根据勾股定理即可求出AF的长;
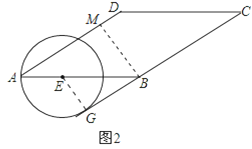
(2)过点B作BM⊥AD于点M,连接EF.利用平行线AD∥CB的性质推知内错角∠DAB=∠ABM;然后在Rt△ABM和Rt△BEG中根据三角函数的定义求得比例式,利用比例的性质即可求得AE的值.
解:(1)设AD和圆相交于F,连接BF,
∵AB是圆的直径,
∴∠AFB=90°,
∴BF⊥AD,
∵AD与BC之间的距离为6,
∴BF=6,
∴AB=10,
∴AF=![]() =8;
=8;
(2)过点B作BM⊥AD于点M,连接EG.
∵AD与BC之间的距离为6,
∴BM=6;
∴sin∠DAB=![]() =
=![]() ;
;
又∵CG是⊙E的切线,
∴EG⊥CG,
∴cos∠BEG=![]() ;
;
∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABG(两直线平行,内错角相等);
∵AE=EG(⊙E的半径),
∴![]()
即![]() ,
,
∴AE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目