题目内容
如图,梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点E、F,且PA=PD.
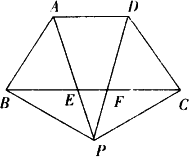
(1)写出图中三对你认为全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
答案:
解析:
解析:
|
(1)①△ABP≌△DCP ②△ABE≌△DCF ③△BEP≌△CFP ④△BFP≌△CEP; (2)求证:△ABP≌△DCP. 证明:∵AD∥BC,AB=DC,∴梯形ABCD为等腰梯形,∴∠BAD=∠CDA. 又∵PA=PD,∴∠BAD-∠PAD=∠CDA-∠PDA,即∠BAP=∠CDP 在△ABP和△DCP中 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
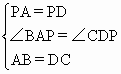 ,∴△ABP≌△DCP.
,∴△ABP≌△DCP. 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.