题目内容
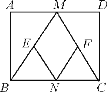
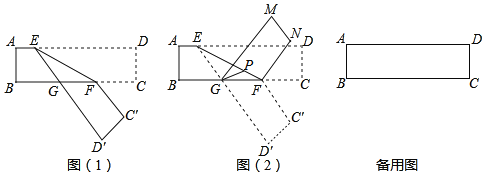
【题目】如图为长方形纸带,AD平行BC,E、F分别是边AD、BC上一点,∠DEF=α,α为锐角且α≠60°,将纸带沿EF折叠如图(1),再由GF折叠如图(2),若GP平分∠MGF交直线EF于点P,则∠GPE=_____(含α的式子表示)
【答案】2α
【解析】
由长方形的对边是平行的,得到∠BFE=∠DEF=α,根据三角形外角的性质得到∠EGB=∠BFE+∠D′EF=2α,由对顶角的性质得到∠FGD′=∠EGB=2α,由折叠可得∠MGF=∠D′GF=2α,由角平分线的定义得到∠PGF=α,再根据三角形外角的性质得到∠GPE.
解:由折叠可得∠GEF=∠DEF,
∵长方形的对边是平行的,
∴∠BFE=∠DEF=α,
∴∠EGB=∠BFE+∠D′EF=2α,
∴∠FGD′=∠EGB=2α,
由折叠可得∠MGF=∠D′GF=2α,
∵GP平分∠MGF,
∴∠PGF=α,
∴∠GPE=∠PGF+∠BFE=2α.
故答案为:2α.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
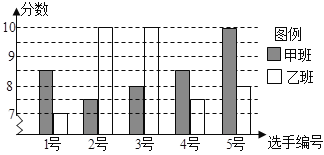
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.