题目内容
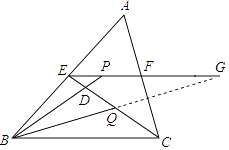
【题目】如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP= . 
【答案】8
【解析】解:如图,延长EF交BQ的延长线于G.
∵EG∥BC,
∴∠G=∠GBC,
∵∠GBC=∠GBP,
∴∠G=∠PBG,
∴PB=PG,
∴PE+PB=PE+PG=EG,
∵3CQ=EC,
∴EQ=2CQ,
∵EG∥BC,
∴ ![]() =
= ![]() =2,∵BC=4,
=2,∵BC=4,
∴EG=8,
∴EP+PB=EG=8,
所以答案是:8.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量(m3) | 38 | 36 | 34 | 32 | … |
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t



