Question

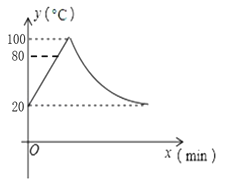
【题目】某品牌的饮水机的运作程序：开机后，20℃的水经过热交换器吸收热能，以每分钟上升6℃的速度加热到80℃，再进入开水器，以每分钟上升10℃的速度从80℃加热到100℃，停止加热，水温下降，此时水温与开机后用时成反比例关系，直至水温降至20℃，开机后进入此程序的整个过程中，水温y（℃）与开机后用时x（min）之间的函数图象如图所示，求在这个过程中：

（1）水温第一次达到80℃的时间；

（2）经过热交换器过程中，y关于x的函数表达式与水温下降过程中，y关于x的函数表达式；

（3）水温不低于20℃且不超过50℃的时间段．

Answer 1

【答案】（1）10min；（2）y1=6x+20 （0≤x≤10） ；；（3）0≤x≤5或 24≤x≤60．

【解析】

（1）根据每分钟上升6℃直接列式计算；

（2）求出一次函数图象过点（0，20）和（10，80），反比例函数解析式过点（12，100），用待定系数法分别求出y关于x的函数表达式即可；

（3）分别将y=50代入一次函数和反比例函数解析式，求出相应的x的值，即可得出结果.

解：（1）由题意得：(80－20)÷6=10(min)，

∴水温第一次达到80℃的时间是10min；

（2）设热交换器过程中，y关于x的函数表达式为：y1=kx+b（k≠0），

∵函数图像过点（0，20）和（10，80），

∴，解得：，

∴热交换器过程中，y1关于x的函数表达式为：y1=6x+20（0≤x≤10）；

(100-80)÷10=2min，2+10=12，

∴反比例函数图像过点（12，100）

设水温下降过程中，y2关于x的函数表达式为：，

将点（12，100）代入可得：k=12×100=1200，

∴，

当y2=20时，x=60，

∴水温下降过程中，y关于x的函数表达式为： ；

（3）将y=50代入y1=6x+20可得：x=5，

将y=50代入可得：x=24，

∴当0≤x≤5或 24≤x≤60时水温不低于20℃且不超过50℃.