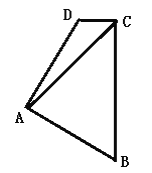
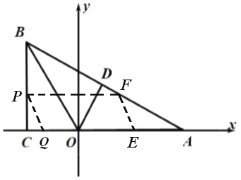
题目内容
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,在
,在![]() 轴正半轴上截取
轴正半轴上截取![]() ,连接
,连接![]() .
.
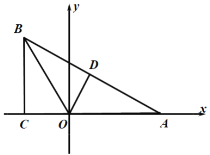
(1)求![]() 点的坐标及
点的坐标及![]() 的解析式;
的解析式;
(2)过![]() 作
作![]() 于
于![]() ,求证:
,求证:![]() ;
;
(3)![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,在
,在![]() 上取
上取![]() 点,连接
点,连接![]() ,动点
,动点![]() 沿
沿![]() 运动,
运动,![]() 在
在![]() 上的运动速度每秒1个单位长度,
上的运动速度每秒1个单位长度,![]() 在
在![]() 上运动速度每秒2个单位长度,当
上运动速度每秒2个单位长度,当![]() 在何处时,
在何处时,![]() 运动的时间最短?请求出
运动的时间最短?请求出![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)根据题意易得点A的坐标,设![]() 解析式为
解析式为![]()
![]() ,然后利用待定系数法确定函数关系式即可;
,然后利用待定系数法确定函数关系式即可;
(2)利用勾股定理求得AB的长,进而得到∠A=30°,然后通过“边角边”证明![]() ;
;
(3)如图过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,由题意得运动时间
,由题意得运动时间![]() ,易证四边形
,易证四边形![]() 为平行四边形,当PQ=CP时即当且仅当
为平行四边形,当PQ=CP时即当且仅当![]() ,
,![]() 横坐标相等时t取最小值,然后求得F坐标即可.
横坐标相等时t取最小值,然后求得F坐标即可.
解:(1)∵![]() ,
,
∴![]() ,
,
设![]() 解析式为
解析式为![]()
![]() ,
,
由题意得 ,
,
解得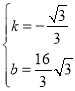 ,
,
∴AB的解析式为![]() ;
;
(2)![]() ,
,
∴![]()
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 与
与![]() 中
中
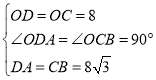 ,
,
∴![]() ;
;
(3)运动时间![]() ,
,
过![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于
轴于![]() ,
,
∴![]() ,
,
∴![]() ,
,
易证四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
故![]() ,此时
,此时![]() .
.

练习册系列答案
相关题目