Question

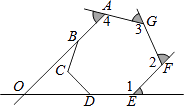
【题目】如图，已知A、O、B三点在同一条直线上，OD平分∠AOC，OE平分∠BOC．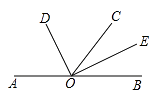

（1）若∠BOC=62°，求∠DOE的度数；
（2）若∠BOC=a°，求∠DOE的度数；
（3）图中是否有互余的角？若有请写出所有互余的角．

Answer 1

【答案】
（1）解：∵OD平分∠AOC，OE平分∠BOC，

∴∠DOC= ∠AOC，∠COE= ∠BOC

∴∠DOE=∠DOC+∠COE= （∠BOC+∠COA）= ×（62°+180°-62°）=90°

（2）解：∠DOE= （∠BOC+∠COA）= ×（a°+180°-a°）=90°
（3）解：∠DOA与∠COE互余；∠DOA与∠BOE互余；∠DOC与∠COE互余；∠DOC与∠BOE互余

【解析】（1）根据角平分线的定义得出∠DOC= ∠AOC，∠COE= ∠BOC，然后根据∠DOE=∠DOC+∠COE= （∠BOC+∠COA）得出答案；
（2）∠DOE的度数其实与角∠BOC的度数无关，∠DOE= （∠BOC+∠COA）=180=90；
（3）根据互为余角的定义相加得90的两个角叫做互为余角，于是得到∠DOA与∠COE互余；∠DOA与∠BOE互余；∠DOC与∠COE互余；∠DOC与∠BOE互余。