题目内容
如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度.已知动点A、B的速度比为1∶3(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,
OB=2OA.
【答案】
解:(1)设动点A的速度是x单位长度/秒,
根据题意得2(x+3x)=16
∴8x=16,
解得:x=2,
则3x=6.
答:动点A的速度是2单位长度/秒,动点B的速度是6单位长度/秒;
(2)标出A,B点如图,
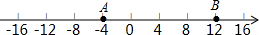
(3)设x秒时,OB=2OA,
当B在A的右边,
根据题意得:12-6x=2(4+2x),
∴x=0.4,
当A在B的右边,
根据题意得:6x-12=2(4+2x),
∴x=10
∴0.4,10秒时OB=2OA.
【解析】(1)设动点A的速度是x单位长度/秒,那么动点B的速度是3x单位长度/秒,然后根据2秒后,两点相距16个单位长度即可列出方程解决问题;
(2)根据(1)的结果和已知条件即可得出.
(3)此问分两种情况讨论:设经过时间为x后,B在A的右边,,若A在B的右边,列出等式解出x即可;

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目



 (速度单位:单位长度/秒)
(速度单位:单位长度/秒)