题目内容
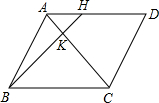如图，H是?ABCD的边AD上一点，且AH=| 1 |
| 2 |
分析：利用平行四边形的性质：对边平行且相等可得AH：BC的值，又因为△AHK∽△CBK，再利用相似的性质即可求出AK和KC的比值．
解答：解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵AH=
HD，
∴AH=
AD=
BC，
∴
=
，
∵AD∥BC，
∴△AHK∽△CBK，
∴
=
=
故选C．
∴AD∥BC，AD=BC，
∵AH=
| 1 |
| 2 |
∴AH=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| AH |
| BC |
| 1 |
| 3 |
∵AD∥BC，
∴△AHK∽△CBK，
∴
| AK |
| KC |
| AH |
| BC |
| 1 |
| 3 |
故选C．
点评：本题考查了平行四边形的性质和相似三角形的判定和相似三角形的性质，题目难度不大，属于基础性题．
练习册系列答案
相关题目
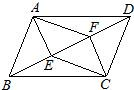24、如图，BD是?ABCD的对角线，AE⊥BD于E，CF⊥BD于F，求证：四边形AECF为平行四边形．
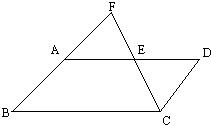3、如图，E是?ABCD的边AD的中点，CE与BA的延长线交于点F，若∠FCD=∠D，则下列结论不成立的是（ ）
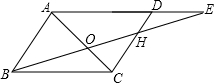（1997•西宁）如图，E是?ABCD的AD边延长线上一点，图中共有相似三角形
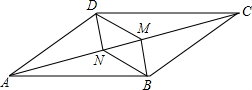如图，AC是?ABCD的一条对角线，BM⊥AC，DN⊥AC，垂足分别为M、N，四边形BMDN是平行四边形吗？请说明理由．