题目内容
 24、如图,BD是?ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.
24、如图,BD是?ABCD的对角线,AE⊥BD于E,CF⊥BD于F,求证:四边形AECF为平行四边形.分析:根据平行四边形的性质可得到AB=CD,AB∥CD,从而可得到∠1=∠2,根据AAS即可判定△AEB≌△CFD,由全等三角形的性质可得到AE=CF,再根据有一组边平行且相等的四边形是平行四边形证得结论.
解答: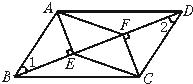 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠1=∠2,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴AECF为平行四边形.
 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠1=∠2,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴AECF为平行四边形.
点评:此题主要考查平行四边形的判定及性质及全等三角形的判定与性质的综合运用.

练习册系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=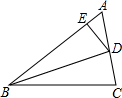 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是