题目内容
【题目】如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值.
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.
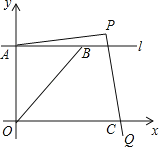
【答案】(1)、PA=2;(2)、1:1;(3)、16.
【解析】
试题分析:(1)、根据点P与点B重合,得出PA的长度;(2)、过点P作PM⊥x轴,过点P作PN⊥y轴,根据点A的纵坐标和点B的横坐标相等得出OA=OB,根据∠OAB=90°可得∠AOB=∠ABO=45°,结合角度之间的关系得出△ANP和△CMP全等得出PA=PC,从而得到比值;(3)、根据∠ANP=∠MON=∠OMP =90°得出四边形OMPN为矩形,根据PM=PN得出四边形OMPN为正方形,根据OA=AB=3,得出OB、BP、OP的长度,根据△ANP和△CMP全等得出四边形的面积.
试题解析:(1)、∵点P与点B重合,点B的坐标是(2,1), ∴点P的坐标是(2,1). ∴PA的长为2.
(2)、过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示
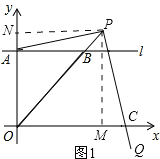 ∵点A的纵坐标与点B的横坐标相等, ∴OA=AB. ∵∠OAB=90°,
∵点A的纵坐标与点B的横坐标相等, ∴OA=AB. ∵∠OAB=90°,
∴∠AOB=∠ABO=45° ∵∠AOC=90°, ∴∠POC=45° ∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP =90° ∴∠NPM=90° ∵∠APC=90° ∴∠APN=90°﹣∠APM=∠CPM
在△ANP和△CMP中, ∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP, ∴△ANP≌△CMP.
∴PA=PC. ∴PA:PC的值为1:1
(3)、∵∠ANP=∠MON=∠OMP =90° ∴四边形OMPN为矩形 ∵PM=PN ∴四边形OMPN为正方形
∵∠OAB=90°,OA=AB=3 ∴OB=![]() ∵OB:BP=3:1 ∴BP=
∵OB:BP=3:1 ∴BP=![]() ∴OP=
∴OP=![]()
∴![]() 正方形OMPN=
正方形OMPN=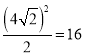 ∵△ANP≌△CMP. ∴S△ANP≌S△CMP. ∴
∵△ANP≌△CMP. ∴S△ANP≌S△CMP. ∴![]() 四边形AOCO=
四边形AOCO=![]() 正方形OMPN=16
正方形OMPN=16

【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
时速数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | ___ |
50﹣60 | ___ | 0.39 |
60﹣70 | ___ | ___ |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
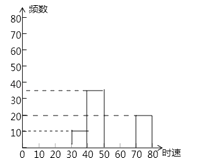
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速超过60千米即为违章,则这次检测到的违章车辆共有 辆.
