题目内容
【题目】已知:在△ABC中,∠ABC=3∠C,∠BAC的平分线AD交BC于D,BE⊥AD于E.
(1)如图l,求证:AC﹣AB=2BE.
(2)如图2,将∠DCA沿直线AC翻折,交BA的延长线于点M,连接MD交AC于点N;MA=BA,BE=1,AB=![]() ,求AN的长.
,求AN的长.

【答案】(1)见解析;(2)2-![]() .
.
【解析】
(1)延长BE交AC于F.由AD平分∠BAC得∠1=∠2,再由BE⊥AD及公共边AE可证△AEB≌△AEF,由全等的性质可知AB=AF,∠3=∠4,BE=FE,则BF=2BE;由三角形外角和可知∠4=∠5+∠C,则∠ABC=∠3+∠5=∠4+∠5=2∠5+∠C,再由∠ABC=3∠C可知∠5=∠C,则CF=BF=2BE,据此即可证明;
(2)作AH⊥BC于H,AK⊥CM于K,易证△AHB≌△AKM,据此可证明△BCA≌△MCA,可得∠CAB=∠CAM=![]() ;再由勾股定理计算可得AE=BE=1,由题干条件及上问证明可得AB=AD,从而得到MD⊥BC,进而得到∠NCD=∠BMD;再通过△AEB是直角等腰三角形可证明△MDC也是直角等腰三角形,可证明△MBD≌△CND,则可通过计算AC和CN的长度,通过AN=AC﹣CN进行计算.
;再由勾股定理计算可得AE=BE=1,由题干条件及上问证明可得AB=AD,从而得到MD⊥BC,进而得到∠NCD=∠BMD;再通过△AEB是直角等腰三角形可证明△MDC也是直角等腰三角形,可证明△MBD≌△CND,则可通过计算AC和CN的长度,通过AN=AC﹣CN进行计算.
解:(1)延长BE交AC于F.
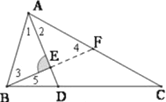
∵AD平分∠BAC,
∴∠1=∠2.
∵BE⊥AD,
∴∠AEB=AEF=90°.
∵∠1=∠2,∠AEB=AEF=90°,AE=AE,
∴△AEB≌△AEF(ASA)
∴AB=AF,∠3=∠4,BE=FE,
∴BF=2BE.
∵∠4=∠5+∠C,
∴∠3=∠5+∠C,
∵∠ABC=∠3+∠5,
∴∠ABC=∠5+∠C+∠5=2∠5+∠C=3∠C,
∴∠5=∠C,
∴CF=BF=2BE.
∵AC﹣AF=FC,
∴AC﹣AB=2BE;
(2)作AH⊥BC于H,AK⊥CM于K,
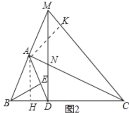
∵∠ACH=∠ACK,
∴AH=AK,
∵AB=AM,
∴△AHB≌△AKM,
∴∠ABH=∠AMK,
∴CB=CM,
∵AC=AC,CB=CM,AB=AM,
∴△BCA≌△MCA,
∴∠CAB=∠CAM=![]() ,
,
∵BE⊥AD,
∴∠AEB=90°.
∵BE=1,AB=![]() ,由勾股定理,得
,由勾股定理,得
∴AE=1,
∴AE=BE,
∴∠BAE=∠ABE
由上问证明可知,∠BAN=∠CAD,∠EBD=∠ACB,
∴∠ABD=∠ABE+∠EBD,∠ADB=∠CAD+∠ACB,
∴∠ABD=∠ADB,
∴AB=AD,
∵AM=AB,
∴AD=AB=AM,
∴△DBM是直角三角形,
∵∠MBD+∠NCD=90°,∠MBD+∠BMD=90°,
∴∠NCD=∠BMD,
∵BE⊥AD,AE=BE,
∴∠BAE=∠ABE=45°.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=90°,
∴∠ABC+∠ACB=90°.
∵∠ABC=3∠ACB,
∴∠ACB=22.5°,
∴∠BCM=45°,
∴∠DMC=45°,
∴∠BCM=∠DMC,
∴DM=DC.
∵∠BDM=∠CDM=90°,DM=DC,∠BMD=∠NCD,
∴△MBD≌△CND(ASA),
∴CN=BM=2AB=2![]() ,
,
∴AC=2BE+AB=2+![]() ,
,
∴AN=AC﹣CN=2﹣![]() .
.










