题目内容
图a是矩形纸片，∠SAB=20°，将纸片沿AB折叠成图b，再沿BN折叠成图c，则图c中的∠TBA的度数是（ ）
分析：首先根据MS∥NT，∠SAB=20°可得∠ABN=20°，再根据折叠方法可得图b中∠ABT=180°-20°=160°，再一次折叠可得图c中∠ABT=140°-20°=120°．
解答：解：∵如图a，MS∥NT，∠SAB=20°，
∴∠ABN=20°，
∴∠ABT=180°-20°=160°，
∴将纸片沿AB折叠成图b时，如图b，∠NBT=160°-20°=140°，
再沿BN折叠成图c，则∠ABT=140°-20°=120°．
故选：A．
∴∠ABN=20°，
∴∠ABT=180°-20°=160°，
∴将纸片沿AB折叠成图b时，如图b，∠NBT=160°-20°=140°，
再沿BN折叠成图c，则∠ABT=140°-20°=120°．
故选：A．
点评：此题主要考查了图形的翻折变换，关键是看懂图中的折叠方法，找准翻折过程中相等的角．
练习册系列答案
相关题目
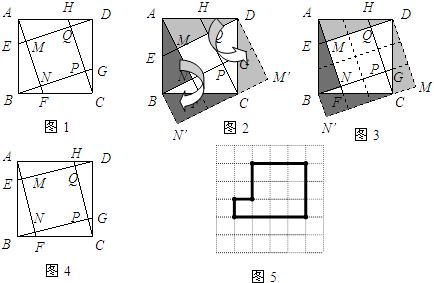
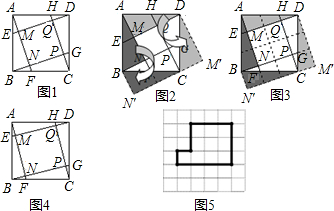
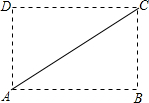（2012•荆州模拟）如图ABCD是矩形纸片，翻折∠B、∠D使BC边、AD边恰好落在AC上，设F、H分别是B、D落在AC上的两点，E、G分别是折痕CE、AG与AB、CD的交点．
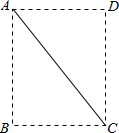如图ABCD是矩形纸片，AC是对角线，把三角形ABC沿AC翻折，点B落到点E处，连接DE