Question

【题目】如图， 中， 为 上一点， 则 的长是（ ）

A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：如图，过点D作DEAC于点E，过点B作BFAC于点F，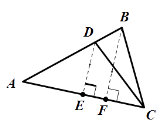

∵ ADC 中，AD=DC=8， ∴ ADC 是等腰三角形，
又∵DEAC，∴AE=EC
设FC=x，AE=EC=y，则EF=EC-FC=y-x，
由作图可知，DEBF，∴ ， 即： ①，
在RtBFC中，∵sin∠BCA=,∴∠BCA=60 ， ∴BF= ，
∵DEBF，∴ADEABF，∴ ， 即： ， ∴DE= ，
在RtADE中，根据勾股定理有：AE2+DE2=AD2 ， 即：y2+（）2=82 ②，
①②两式联立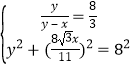： ， 解得： ，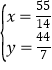
∴AC=2AE=2y=2=.
故选D.
【考点精析】本题主要考查了勾股定理的概念和相似三角形的判定与性质的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．