题目内容
若规定一种新运算为a?b=
+
,如果2?
=-1,那么2001?2002=
.
| 1 |
| ab |
| 1 |
| (a-1)(b+A) |
| 1 |
| 2 |
| 1 |
| 2002000 |
| 1 |
| 2002000 |
分析:由2?
=-1,利用题中的新定义确定出A的值,然后再利用新定义表示出所求的式子,把A的值代入后,利用拆项法变形后合并抵消,最后通分后,利用同分母分数的加法法则计算即可得出结果.
| 1 |
| 2 |
解答:解:由2?
=-1,根据题意得:
+
=-1,
解得:A=-1,
则2001?2002=
+
=
-
+
-
=
-
=
.
故答案为:
| 1 |
| 2 |
| 1 | ||
2×
|
| 1 | ||
(2-1)(
|
解得:A=-1,
则2001?2002=
| 1 |
| 2001×2002 |
| 1 |
| 2000×2001 |
| 1 |
| 2001 |
| 1 |
| 2002 |
| 1 |
| 2000 |
| 1 |
| 2001 |
| 1 |
| 2000 |
| 1 |
| 2002 |
| 1 |
| 2002000 |
故答案为:
| 1 |
| 2002000 |
点评:此题考查了有理数的混合运算,是一道新定义的题.此类题是近年来中考的热点题型.理解新定义,确定出A的值是解本题的关键,最后计算时注意利用拆项的方法来简化运算.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
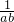 +
+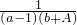 ,如果2?
,如果2? =-1,那么2001?2002=________.
=-1,那么2001?2002=________.