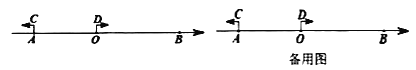题目内容
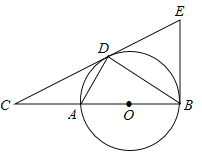
【题目】如图,点![]() 是直线
是直线![]() 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点![]() 作射线
作射线![]() 平分
平分![]() .
.

(1)如图1,如果![]() ,依题意补全图形,求
,依题意补全图形,求![]() 度数;
度数;
(2)当直角三角板绕点![]() 顺时针旋转一定的角度得到图2,使得直角边
顺时针旋转一定的角度得到图2,使得直角边![]() 在直线
在直线![]() 的上方,若
的上方,若![]() ,其他条件不变,请你直接用含
,其他条件不变,请你直接用含![]() 的代数式表示
的代数式表示![]() 的度数为 ;
的度数为 ;
(3)当直角三角板绕点![]() 继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现
继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现![]() 与
与![]()
![]()
![]() 之间有怎样的数量关系?请直接写出你的发现: .
之间有怎样的数量关系?请直接写出你的发现: .
【答案】(1)补全图形见解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]() .
.
【解析】
(1)根据角平分线的作法作出OE平分∠BOC,先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(2)先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(3)分两种情况:0°≤∠AOC≤180°,0°≤∠DOE≤180°,可求∠AOC与∠DOE之间的数量关系.
(1)补全图形:
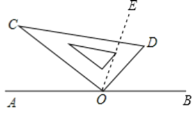
解:因为![]()
所以![]()
因为![]() 平分
平分![]() ,
,
所以![]() ;
;
由直角三角板,得![]() ;
;
因为![]() ;
;
所以![]() ;
;
(2)∵由∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°-α;
∵OE平分∠BOC,
∴∠COE=90°-![]() α;
α;
∵直角三角板,
∴∠COD=90°;
∵∠COD=90°,∠COE=90°-![]() α,
α,
∴∠DOE=![]() ;
;
(3)①0°≤∠AOC≤180°时,
∵由∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC;
∵OE平分∠BOC,
∴∠COE=90°-![]() ∠AOC;
∠AOC;
∵直角三角板,
∴∠COD=90°;
∵∠COD=90°,∠COE=90°-![]() ∠AOC,
∠AOC,
∴∠DOE=![]() ∠AOC;
∠AOC;
②0°≤∠DOE≤180°时,
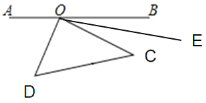
∵由∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC;
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=90°-
∠BOC=90°-![]() ∠AOC;
∠AOC;
∵直角三角板,
∴∠COD=90°;
∴∠DOE=90°+∠COE =180°-![]() ∠AOC;
∠AOC;
∴∠DOE=![]() ∠AOC(0°≤∠AOC≤180°),∠DOE=180°
∠AOC(0°≤∠AOC≤180°),∠DOE=180°![]() ∠AOC(0°≤∠DOE≤180°).
∠AOC(0°≤∠DOE≤180°).

 名校课堂系列答案
名校课堂系列答案【题目】我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确数字x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.

调查结果统计表
组别 | 分组 | 人数 |
A |
| 4 |
B |
| 16 |
C |
| a |
D |
| b |
E |
| 2 |
请根据以上图表,解答下列问题:
![]() 填空:这次被调查的同学共有______ 人,
填空:这次被调查的同学共有______ 人, ![]() ______ ,
______ , ![]() ______ ;
______ ;
![]() 求扇形统计图中扇形C的圆心角度数;
求扇形统计图中扇形C的圆心角度数;
![]() 该校共有学生1000人,请估计每月零花钱的数额x在
该校共有学生1000人,请估计每月零花钱的数额x在![]() 范围的人数.
范围的人数.