��Ŀ����
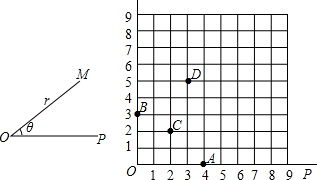
��ͼ����ƽ��ֱ������ϵ�У���֪����A��0��a����B��b��0����C��b��c��������a��b��c�����ϵʽ|a-2|+��b-3��2=0��c=2b-a��
��1����a��b��c��ֵ��
��2������ٵڶ���������һ��P��m��1�������ú�m��ʽ�ӱ�ʾ�ı���ABOP����������ı���ABOP��������ABC�������ȣ��������P�����ꣻ
��3����B��A����ֱ���x�ᣬy������������˶������BAO���ڲ��ǵ�ƽ���ߺ͡�ABO���ڲ��ǵ�ƽ�����ཻ�ڵ�һ������һ��Q����ô����A��B���˶��Ĺ����У���Q�Ĵ�С�Ƿ�ᷢ���仯�����������仯���������ֵ���������仯����˵�����ɣ�

��1����a��b��c��ֵ��
��2������ٵڶ���������һ��P��m��1�������ú�m��ʽ�ӱ�ʾ�ı���ABOP����������ı���ABOP��������ABC�������ȣ��������P�����ꣻ
��3����B��A����ֱ���x�ᣬy������������˶������BAO���ڲ��ǵ�ƽ���ߺ͡�ABO���ڲ��ǵ�ƽ�����ཻ�ڵ�һ������һ��Q����ô����A��B���˶��Ĺ����У���Q�Ĵ�С�Ƿ�ᷢ���仯�����������仯���������ֵ���������仯����˵�����ɣ�

��1����|a-2|+��b-3��2=0��
��a-2=0��b-3=0��
��a=2��b=3��
�֡�c=2b-a��
��c=2��3-2=4��
��2�������⣺S��ABC=
BC��b=
��4��3=6��
S�ı���ABOP=
��AO��|m|+
��AO��|c|=
��2��|m|+
��2��3=|m|+3��
������S�ı���ABOP=S��ABC��
��|m|+3=6��
��m=��3��
�ߵ�P�ڵڶ����ޣ�
���P��-3��1����
��3����AQBΪ��ֵ��
֤������2��BAQ=��AOB+��ABO��2��ABQ=��AOB+��OAB��
��2����BAQ+��ABQ��=2��AOB+��ABO+��OAB��
��BAQ+��ABQ=��AOB+
=90��+
��AOB��
�ߡ�AOB��СΪ��ֵ��
���BAQ+��ABQ�Ĵ�СΪ��ֵ��
���AQB=180��-����BAQ+��ABQ����
�ʡ�AQBΪ��ֵ��
��a-2=0��b-3=0��
��a=2��b=3��
�֡�c=2b-a��
��c=2��3-2=4��
��2�������⣺S��ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S�ı���ABOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
������S�ı���ABOP=S��ABC��
��|m|+3=6��
��m=��3��
�ߵ�P�ڵڶ����ޣ�
���P��-3��1����
��3����AQBΪ��ֵ��
֤������2��BAQ=��AOB+��ABO��2��ABQ=��AOB+��OAB��
��2����BAQ+��ABQ��=2��AOB+��ABO+��OAB��
��BAQ+��ABQ=��AOB+
| 180��-��AOB |
| 2 |
| 1 |
| 2 |
�ߡ�AOB��СΪ��ֵ��
���BAQ+��ABQ�Ĵ�СΪ��ֵ��
���AQB=180��-����BAQ+��ABQ����
�ʡ�AQBΪ��ֵ��

��ϰ��ϵ�д�
�����Ŀ