题目内容
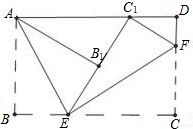将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，AB=| 3 |
分析：△ABE和△AB1E对折，两三角形全等，△EC1F和△ECF对折，两三角形也全等，根据边角关系求出BC．
解答：解：∵△ABE和△AB1E对折，
∴△ABE≌△AB1E，
∴BE=B1E，∠B=∠AB1E=90°，
∵∠BAE=30°，AB=
，
∴BE=1，
∵△AB1C1≌△AB1E，
∴AC1=AE，
又∵∠AEC1=∠AEB=60°
∴AEC1是等边三角形，EC1=AE=2
∵EC=EC1=2，
∴BC=2+1=3．
∴△ABE≌△AB1E，
∴BE=B1E，∠B=∠AB1E=90°，
∵∠BAE=30°，AB=
| 3 |
∴BE=1，
∵△AB1C1≌△AB1E，
∴AC1=AE，
又∵∠AEC1=∠AEB=60°
∴AEC1是等边三角形，EC1=AE=2
∵EC=EC1=2，
∴BC=2+1=3．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．
练习册系列答案
精英口算卡系列答案
相关题目
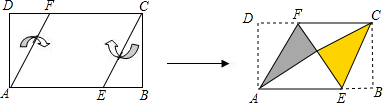
将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
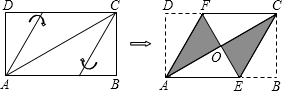C的长为
