题目内容
（2012•锦州二模）将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=6，则BC的长为
2
| 3 |
2
．| 3 |
分析：根据菱形AECF，得∠FCO=∠ECO，再利用∠ECO=∠ECB，可通过折叠的性质，结合直角三角形勾股定理求解．
解答：解：∵菱形AECF，AB=6，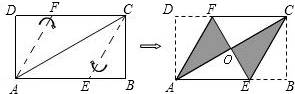
∴假设BE=x，
∴AE=6-x，
∴CE=6-x，
∵四边形AECF是菱形，
∴∠FCO=∠ECO，
∵∠ECO=∠ECB，
∴∠ECO=∠ECB=∠FCO=30°，
2BE=CE，
∴CE=2x，
∴2x=6-x，
解得：x=2，
∴CE=4，利用勾股定理得出：
BC2+BE2=EC2，
BC=
=
=2
，
故答案为：2
．
∴假设BE=x，
∴AE=6-x，
∴CE=6-x，
∵四边形AECF是菱形，
∴∠FCO=∠ECO，
∵∠ECO=∠ECB，
∴∠ECO=∠ECB=∠FCO=30°，
2BE=CE，
∴CE=2x，
∴2x=6-x，
解得：x=2，
∴CE=4，利用勾股定理得出：
BC2+BE2=EC2，
BC=
| EC2-BE2 |
| 42-22 |
| 3 |
故答案为：2
| 3 |
点评：此题主要考查了折叠问题以及勾股定理等知识，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
（2012•锦州二模）如图是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，那么这个几何体的主视图是（ ）
（2012•锦州二模）如图，在直角坐标系中．Rt△ABC位于第一象限，两条直角边AB、BC分别平行于x轴、y轴，顶点B的坐标为（2，4），AB=1，BC=2．