题目内容
【题目】如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化. 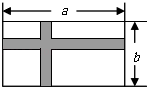
(1)求出绿地的面积;(用含a、b的代数式表示)
(2)若a=2b,且道路的面积为116米2 , 求原长方形空地的宽.
【答案】
(1)解:∵长方形空地的长为a米、宽为b米,中间有两条互相垂直的宽均为2米的道路,
∴绿地的面积是:(a﹣2)(b﹣2)米2
(2)解:根据题意得:  ,
,
解得 ![]() ,
,
答:原长方形空地的宽为20米
【解析】(1)根据长方形空地的长为a米、宽为b米,中间有两条互相垂直的宽均为2米的道路,再根据长方形的面积公式即可得出答案;(2)根据长方形的长是宽的2倍和长方形的面积=绿地的面积+道路的面积,列出方程组,进行求解即可.

练习册系列答案
相关题目
【题目】已知一次函数y=﹣2x﹣4
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?



