题目内容
【题目】在平面直角坐标系中，二次函数y=ax2+
x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y=﹣
x+2与二次函数图象在第一象限内的交点．
（1）求二次函数的解析式及点E的坐标．
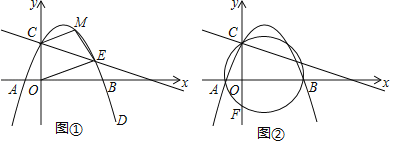
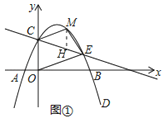
（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．
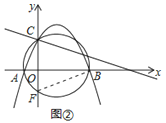
（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．
【答案】（1）E（3，1）；（2）S最大=
，M坐标为（
，3）；（3）F坐标为（0，﹣）．
【解析】
1）把C与D坐标代入二次函数解析式求出a与c的值，确定出二次函数解析式，与一次函数解析式联立求出E坐标即可；
（2）过M作MH垂直于x轴，与直线CE交于点H，四边形COEM面积最大即为三角形CME面积最大，构造出二次函数求出最大值，并求出此时M坐标即可；
（3）令y=0，求出x的值，得出A与B坐标，由圆周角定理及相似的性质得到三角形AOC与三角形BOF相似，由相似得比例求出OF的长，即可确定出F坐标．
（1）把C（0，2），D（4，﹣2）代入二次函数解析式得：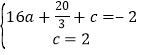
，
解得：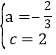
，即二次函数解析式为y=﹣
x2+
x+2，
联立一次函数解析式得：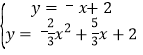
，
消去y得：﹣
x+2=﹣x2+x+2，
解得：x=0或x=3，
则E（3，1）；
（2）如图①，过M作MH∥y轴，交CE于点H，
设M（m，﹣m2+m+2），则H（m，﹣m+2），
∴MH=（﹣m2+m+2）﹣（﹣m+2）=﹣m2+2m，
S四边形COEM=S△OCE+S△CME=
×2×3+MH3=﹣m2+3m+3，
当m=﹣
=时，S最大=，此时M坐标为（，3）；
（3）连接BF，如图②所示，
当﹣x2+x+20=0时，x1=
，x2=
，
∴OA=
，OB=，
∵∠ACO=∠ABF，∠AOC=∠FOB，
∴△AOC∽△FOB，
∴
，即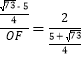
，
解得：OF=，
则F坐标为（0，﹣）．
