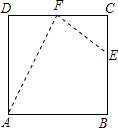
题目内容
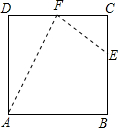 一个工人师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长为a)的余料,修剪成如四边形ABEF的零件.其中
一个工人师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长为a)的余料,修剪成如四边形ABEF的零件.其中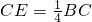 ,F是CD的中点.
,F是CD的中点.
(1)试用含a的代数式表示AF2+EF2的值;
(2)连接AE,则△AEF是直角三角形吗?为什么?
解:(1)连接AE,
则AB=a,BE= a,
a,
∵∠B=90°
∴AE2= ;
;
∵CE:CF=DF:AD=1:2,
∠C=∠D=90°;
∴△ADF∽△FCE,
∴∠CFE+∠AFD=90°
∴∠AFE=90°
∴AF2+EF2=AE2= ;
;
(2)由(1)中AF2+EF2=AE2,
可知△AEF是直角三角形.
分析:先连接AE,证明△ADF∽△FCE,得到∠AFE=90°,所以AF2+EF2=AE2= .
.
点评:主要考查了正方形的性质和直角三角形的判定.注意正方形是特殊条件最多的特殊平行四边形.要掌握正方形的性质和勾股定理的逆定理才会灵活运用.
则AB=a,BE=
 a,
a,∵∠B=90°
∴AE2=
 ;
;∵CE:CF=DF:AD=1:2,
∠C=∠D=90°;
∴△ADF∽△FCE,
∴∠CFE+∠AFD=90°
∴∠AFE=90°
∴AF2+EF2=AE2=
 ;
;(2)由(1)中AF2+EF2=AE2,
可知△AEF是直角三角形.
分析:先连接AE,证明△ADF∽△FCE,得到∠AFE=90°,所以AF2+EF2=AE2=
 .
.点评:主要考查了正方形的性质和直角三角形的判定.注意正方形是特殊条件最多的特殊平行四边形.要掌握正方形的性质和勾股定理的逆定理才会灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
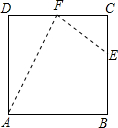 一个工人师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长为a)的余料,修剪成如四边形ABEF的零件.其中
一个工人师傅要将一个正方形ABCD(四个角都是直角,四边都相等,边长为a)的余料,修剪成如四边形ABEF的零件.其中 (四个角都是直角,四边都相等,边长
(四个角都是直角,四边都相等,边长 的余料,修剪成如四边形
的余料,修剪成如四边形 的零件. 其中
的零件. 其中 ,
, 是
是 的中点.
的中点.
 的值;
的值; ,则△
,则△ 是直角三角形吗?为什么?
是直角三角形吗?为什么? (四个角都是直角,四边都相等,边长
(四个角都是直角,四边都相等,边长 的余料,修剪成如四边形
的余料,修剪成如四边形 的零件. 其中
的零件. 其中 ,
, 是
是 的中点.
的中点.
 的值;
的值; ,则△
,则△ 是直角三角形吗?为什么?
是直角三角形吗?为什么?