题目内容
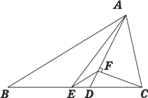
【题目】如图,△ABC中,AB=12,AC=5,AD是∠BAC角平分线,AE是BC边上的中线,
过点C做CF⊥AD于F,连接EF,则线段EF的长为_______.
【答案】3.5.
【解析】首先证明△AGF≌△ACF,则AG=AC=4,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
解:延长CF交AB于点G,

∵AD平分∠BAC,
∴∠GAF=∠CAF,∵CG⊥AD,
∴∠AFG=∠AFC,
在△AGF和△ACF中,∠GAF=∠CAF,AF=AF,∠AFG=∠AFC,
△AGF≌△ACF(ASA),
∴AG=AC=5,GF=CF=7.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=![]() BG=3.5.
BG=3.5.
故答案是:3.5.

练习册系列答案
相关题目