题目内容
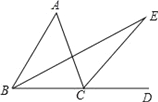
【题目】如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)求∠E的度数.
(2)请猜想∠A与∠E之间的数量关系,请说明理由.
【答案】(1)∠E=20°;(2)∠A=2∠E.理由见解析.
【解析】
(1)由角平分线定义可得∠ABC=2∠CBE,∠ACD=2∠DCE,再根据三角形外角的性质可得∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,从而可得∠A=2∠E,继而可得∠E的度数;
(2)由角平分线定义可得∠ABC=2∠CBE,∠ACD=2∠DCE,再根据三角形外角的性质可得∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,从而可得∠A=2∠E.
(1)∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠CBE,∠ACD=2∠DCE,
由三角形的外角性质得,∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,
∴∠A+∠ABC=2(∠E+∠CBE),
∴∠A=2∠E,
∵∠A=40°,
∴∠E=20°;
(2)∠A=2∠E,理由如下:
∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠CBE,∠ACD=2∠DCE,
由三角形的外角性质得,∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,
∴∠A+∠ABC=2(∠E+∠CBE),
∴∠A=2∠E.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目