题目内容
【题目】如图所示，在正方形ABCD中，M为AB的中点，N为AD上的一点，且AN= 
AD，试猜测△CMN是什么三角形，请证明你的结论．（提示：正方形的四条边都相等，四个角都是直角） 
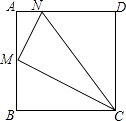
【答案】解：△CMN是直角三角形．理由如下： 设正方形ABCD的边长为4a，则AB=BC=CD=AD=4a．
∵M是AB的中点，
∴AM=BM=2a．
∵AN= 
AD，AD=4a，
∴AN=a，DN=3a．
∵在Rt△AMN中，满足AM2+AN2=MN2 ， 且AM=2a，AN=a，
∴MN= 
a．
同理可得：MC= 
a，NC=5a．
∵MN2+MC2=（ a）2+（ a）2=25a2 ， NC2=（5a）2=25a2 ，
∴MN2+MC2=NC2 ，
∴△CMN是直角三角形
【解析】可设正方形ABCD的边长为4a，利用勾股定理分别求出NC，MN，CM的值，计算得出MN2+MC2=NC2 ， 根据勾股定理的逆定理可判定△CMN是直角三角形．
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
名师点拨卷系列答案
英才计划期末调研系列答案
【题目】为了加强对校内外安全监控，创建荔湾平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格，有效监控半径如表所示，经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．
甲型 | 乙型 | |
价格（元/台） | a | b |
有效半径（米/台） | 150 | 100 |
（1）求a、b的值．
（2）若购买该批设备的资金不超过11000元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？
（3）在（2）问的条件下，若要求监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案．
