题目内容
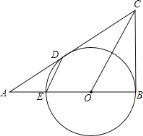
【题目】如图,![]() 、
、![]() 是
是![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() .
.![]() 的延长线与
的延长线与![]() 的直径
的直径![]() 的延长线交于
的延长线交于![]() 点,连接
点,连接![]() ,
,![]() .
.
![]() 探索
探索![]() 与
与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,证明见解析;
,证明见解析;![]() .
.
【解析】
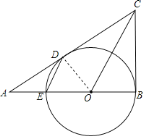
(1)连接OD,证△COD≌△COB,则∠COD=∠COB;又∠DOB是等腰△ODE的外角,则∠DOB=2∠DEB,由此可证得∠COB=∠DEB;同位角相等,则DE∥OC;
(2)Rt△ABC中,由勾股定理,易求得AB的长;然后在Rt△ADO中,用⊙O的半径表示出OA的长,再根据勾股定理求出⊙O的半径.则Rt△COD中,即可求得∠OCD的正切值,由(1)知:∠ADE=∠OCE,由此可求出∠ADE的正切值.
(1)![]() ,
,
连接![]() ,
,
∵![]() 、
、![]() 是
是![]() 的切线,
的切线,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
设![]() 的半径为
的半径为![]() ,
,
在![]() 中有
中有![]()
解得![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目