题目内容
【题目】解决问题时需要思考:是否解决过与其类似的问题.小明从问题1解题思路中获得启发从而解决了问题2.
问题1:如图①,在正方形ABCD中,E、F是BC、CD上两点,∠EAF=45°.
求证:∠AEF=∠AEB.
小明给出的思路为:延长EB到H,满足BH=DF,连接AH.请完善小明的证明过程.

问题2:如图②,在等腰直角△ABC中,∠ACB=90°,AC=BC=4,D为AB中点,E、F是AC、BC边上两点,∠EDF=45°.
(1)求点D到EF的距离.
(2)若AE=a,则S△DEF= (用含字母a的代数式表示).
【答案】(1)证明见解析;(2)2,(3)a+![]() -4
-4
【解析】试题分析:问题1:如图①中,延长EB到H,满足BH=DF,连接AH,只要证明△AHE≌△AFE,即可推出∠AEF=∠AEB;
问题2:(1)如图②中,过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,利用(1)中即可,根据角平分线的性质定理即可解决问题,
(2)在Rt△DEG中,DE=![]() ,由S△AED=
,由S△AED=![]() AEDG=a,△DEF∽△AED,推出
AEDG=a,△DEF∽△AED,推出![]() ,由此即可解决问题;
,由此即可解决问题;
试题解析:问题1:证明:如图①中,延长EB到H,满足BH=DF,连接AH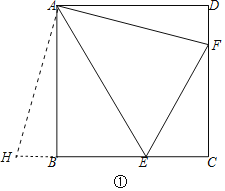
∵AB=AD,∠ABH=∠D=90°,BH=DF,
∴△ADF≌ABH,
∴∠DAF=∠BAH,AF=AH,
∵∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°,
即∠EAH=∠BAH+∠BAE=45°,
∴∠EAH=∠EAF,
又∵AF=AH,AE=AE,
∴△AHE≌△AFE,
∴∠AEF=∠AEB.
问题2:解:(1)过点D分别向AC、BC、EF作垂线,垂足分别为G、H、M,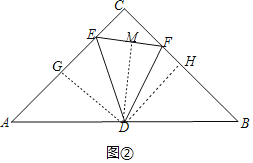
∵∠ACB=90°,∴CGDH为矩形,∵AC=BC=4,D为AB中点,
∴DG=DH=![]() BC=2,
BC=2,
∴四边形CGDH为正方形,
由问题1知∠DEG=∠DEM,
∴DM=DG=2.
(2)在Rt△DEG中,DE=![]() ,
,
∵S△AED=![]() AEDG=a,
AEDG=a,
∵△DEF∽△AED,
∴![]() ,
,
∴S△DEF=![]() .
.