题目内容
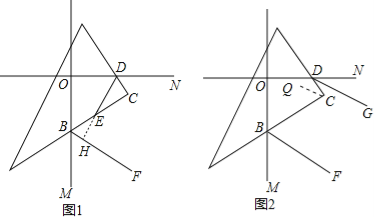
【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:
(3)如图2:若BF、DG分别平分∠OBC、∠ODC的外角,判断BF与DG的位置关系,并说明理由。

【答案】(1)180°;(2)见解析;(3)BF∥DG.
【解析】试题分析:(1)先利用垂直定义得到∠MON=90°,然后利用四边形内角和求解;
(2)延长DE交BF于H,如图,由于∠OBC+∠ODC=180°,∠OBC+∠CBM=180°,根据等角的补角相等得到∠ODC=∠CBM,由于DE平分∠ODC,BF平分∠CBM,则∠CDE=∠FBE,然后根据三角形内角和可得∠BHE=∠C=90°,于是DE⊥BF;
(3)作CQ∥BF,如图2,由于∠OBC+∠ODC=180°,则∠CBM+∠NDC=180°,再利用BF、DG分别平分∠OBC、∠ODC的外角,则∠GDC+∠FBC=90°,根据平行线的性质,由CQ∥BF得∠FBC=∠BCQ,加上∠BCQ+∠DCQ=90°,则∠DCQ=∠GDC,于是可判断CQ∥GD,所以BF∥DG.
(1)解:∵OM⊥ON,
∴∠MON=90°,
在四边形OBCD中,∠C=∠BOD=90°,
∴∠OBC+∠ODC=360°﹣90°﹣90°=180°;
故答案为180°;
(2)证明:延长DE交BF于H,如图1,
∵∠OBC+∠ODC=180°,
而∠OBC+∠CBM=180°,
∴∠ODC=∠CBM,
∵DE平分∠ODC,BF平分∠CBM,
∴∠CDE=∠FBE,
而∠DEC=∠BEH,
∴∠BHE=∠C=90°,
∴DE⊥BF;
(3)解:DG∥BF.理由如下:
作CQ∥BF,如图2,
∵∠OBC+∠ODC=180°,
∴∠CBM+∠NDC=180°,
∵BF、DG分别平分∠OBC、∠ODC的外角,
∴∠GDC+∠FBC=90°,
∵CQ∥BF,
∴∠FBC=∠BCQ,
而∠BCQ+∠DCQ=90°,
∴∠DCQ=∠GDC,
∴CQ∥GD,
∴BF∥DG.