题目内容
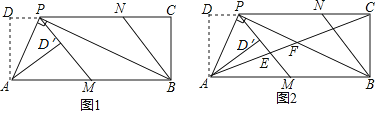
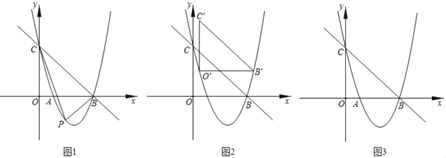
【题目】已知如图:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.

(1)试说明四边形DEAF为平行四边形.
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 .
【答案】(1)见解析;(2)∠BAC=150°时,见解析;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据等边三角形的性质得∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,则∠ABC=∠EBD,于是可利用“SAS”判断△ABC≌△EBD,得到AC=DE,再由△ACF为等边三角形得AC=AF,则AF=DE,同理可证△ACB≌△FCD得到AB=DF,则AE=DF,然后根据平行四边形的判定方法即可得到结论;
(2)由于四边形DEAF是平行四边形,当∠EAF=90°时,四边形DEAF为矩形,根据等边三角形角的大小,可得∠BAC=150°;
(3)由于四边形DEAF是平行四边形,根据菱形的判定方法,当AE=AF时,四边形DEAF是菱形,此时AB=AC.
解:(1)如图1,∵△ABE和△CBD为等边三角形,
∴∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,
∴∠ABC=∠EBD,
在△ABC和△EBD中,
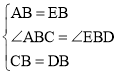 ,
,
∴△ABC≌△EBD(SAS),
∴AC=DE,
∵△ACF为等边三角形,
∴AC=AF,
∴AF=DE,
同理可证得△ACB≌△FCD,
∴AB=DF,
而AB=AE,
∴AE=DF,
∴四边形DEAF是平行四边形;
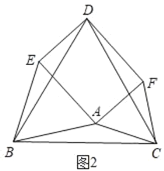
(2)如图2,当△ABC满足∠BAC=150°时,四边形DEAF是矩形.
理由如下:
由(1)知:四边形DEAF是平行四边形,
∵∠BAC=150°,∠EAB=∠FAC=60°
∴∠EAF=360°﹣150°﹣60°﹣60°=90°
∴四边形DEAF是矩形;
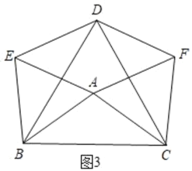
(3)如图3,△ABC满足AB=AC时,四边形DEAF是菱形.
理由如下:
由(1)知:四边形DEAF是平行四边形,
∵AB=AC,AE=AB,AC=AF,
∴AE=AF,
∴四边形DEAF是菱形.
故答案为:AB=AC.


 阅读快车系列答案
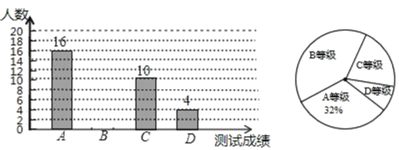
阅读快车系列答案【题目】现实社会中,塑料袋仍然是白色污染的一部分,为了解塑料袋的使用情况,某校八年级环保小组随机抽取“幸福小区”40户居民家庭,记录了这些家庭某个月丢弃塑料袋的数量(单位:个)如下:
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据,解答以下问题:
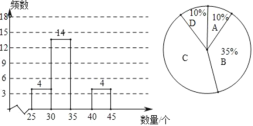
(1)若数据为x,按“组距为5”列出了如下的频数分布表,请将表中空缺的部分补充完整,并补全频数分布直方图;
分组 | 频数 |
A:25≤x<30 | 4 |
B:30≤x<35 | 14 |
C:35≤x<40 | |
D:40≤x<45 | 4 |
合计 | 40 |
(2)根据(1)中的直方图可以看出,这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,画出了如图所示的扇形统计图,请求出C组对应的扇形圆心角的度数;
(4)若该小区共有1000户居民家庭,请你估计每月丢弃的塑料袋数量不小于30个的家庭户数.