Question

【题目】如图，一次函数与反比例函数的图象交于点.

（1）求这两个函数的表达式；

（2）在轴上是否存在点，使为等腰三角形？若存在，求的值，若不存在，说明理由.

Answer 1

【答案】（1）y=，y=-x+1；（2）n=-1+或n=2+.

【解析】

试题分析：（1）将点A代入反比例函数解析式可先求出k2,再求出点B的坐标，再运用待定系数法求k1和b的值；（2）需要分类讨论，PA=PB，AP=AB，BP=BA，运用勾股定理求它们的长，构造方程求出n的值.

试题解析：（1）解：把A（-1,2）代入，得k2=-2，

∴反比例函数的表达式为y=

∵B（m,-1）在反比例函数的图象上，

∴m=2。

由题意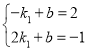得，解得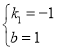

∴一次函数的表达式为y=-x+1。

（2）解：由A（-1,2）和B（2，-1），则AB=3

① 当PA=PB时，（n+1）2+4=(n-2)2+1,

∵n>0，∴n=0（不符合题意，舍去）

②当AP=AB时，22+（n+1）2=(3)2

∵n>0，∴n=-1+

③当BP=BA时，12+（n-2）2=(3)2

∵n>0，∴n=2+

所以n=-1+或n=2+.