题目内容
 如图,有长为30m的篱笆,一面利用墙围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
如图,有长为30m的篱笆,一面利用墙围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.(1)求y与x的函数关系式;
(2)如果墙的最大可用长度为10m,要围成面积为63m2的花圃,AB的长是多少?
分析:(1)设AB的长为xm,则平行一墙的一边长为:(30-3x)m,该花圃的面积为:(30-x)x;进而得出函数关系即可;
(2)令该面积等于63,求出符合题意的x的值,即是所求AB的长.
(2)令该面积等于63,求出符合题意的x的值,即是所求AB的长.
解答:解:(1)由题意得:
y=x(30-3x),即y=-3x2+30x(0<x<10).
(2)当y=63时,-3x2+30x=63.
解此方程得x1=7,x2=3.
当x=7时,30-3x=9<10,符合题意;
当x=3时,30-3x=21>10,不符合题意,舍去;
故当AB的长为7m时,花圃的面积为63m2.
y=x(30-3x),即y=-3x2+30x(0<x<10).
(2)当y=63时,-3x2+30x=63.
解此方程得x1=7,x2=3.
当x=7时,30-3x=9<10,符合题意;
当x=3时,30-3x=21>10,不符合题意,舍去;
故当AB的长为7m时,花圃的面积为63m2.
点评:本题考查了二次函数和一元二次方程的实际应用,根据题目的条件,合理地建立函数关系式是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 m,面积为
m,面积为 与
与 的花圃,
的花圃,
 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 m,面积为
m,面积为 .
. 与
与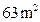 的花圃,
的花圃,