题目内容
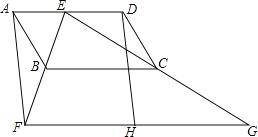
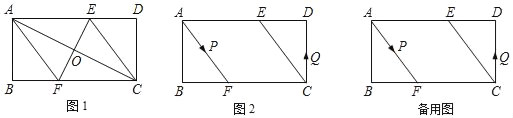
【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.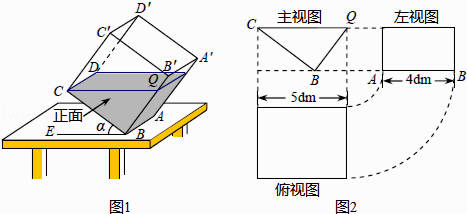
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ![]() ,tan37°=
,tan37°= ![]() )
)
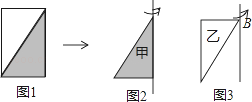
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 . 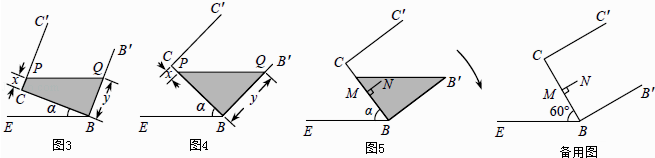
【答案】
(1)CQ∥BE;3
(2)
解:V液= ![]() ×3×4×4=24(dm3)
×3×4×4=24(dm3)
(3)
解:在Rt△BCQ中,tan∠BCQ= ![]() ,
,
∴α=∠BCQ=37°.
当容器向左旋转时,如图3,0°≤α≤37°,
∵液体体积不变,
∴ ![]() (x+y)×4×4=24,
(x+y)×4×4=24,
∴y=﹣x+3.
当容器向右旋转时,如图4.同理可得:y= ![]() ;
;
当液面恰好到达容器口沿,即点Q与点B′重合时,如图5,
由BB′=4,且 ![]() PBBB′×4=24,得PB=3,
PBBB′×4=24,得PB=3,
∴由tan∠PB′B= ![]() ,得∠PB′B=37°.
,得∠PB′B=37°.
∴α=∠B′PB=53°.此时37°≤α≤53°;
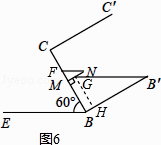
(4)解:当α=60°时,如图6所示,设FN∥EB,GB′∥EB,过点G作GH⊥BB′于点H.
在Rt△B′GH中,GH=MB=2,∠GB′B=30°,
∴HB′=2 ![]() .
.
∴MG=BH=4﹣2 ![]() <MN.
<MN.
此时容器内液体形成两层液面,液体的形状分别是以Rt△NFM和直角梯形MBB′G为底面的直棱柱.
∵S△NFM+SMBB′G= ![]() ×
× ![]() ×1+
×1+ ![]() (4﹣2
(4﹣2 ![]() +4)×2=8﹣
+4)×2=8﹣ ![]() .
.
∴V溢出=24﹣4(8﹣ ![]() )=
)= ![]() ﹣8>4(dm3).
﹣8>4(dm3).
∴溢出液体可以达到4dm3.
【解析】解:(1)CQ∥BE,BQ= ![]() =3;
=3;
【考点精析】掌握矩形的性质是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等.

【题目】今年十一黄金周期间,九寨沟7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化/万人 | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)、请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?(5分)
(2)、如果9月30日旅游人数为2.5万人,平均每人消费500元,请问风景区在此7天内总收入为多少万元?
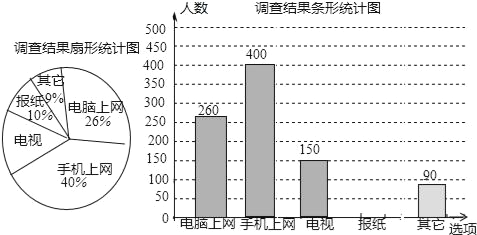
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图. 上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a=;b=;
(2)补全频数分布直方图; 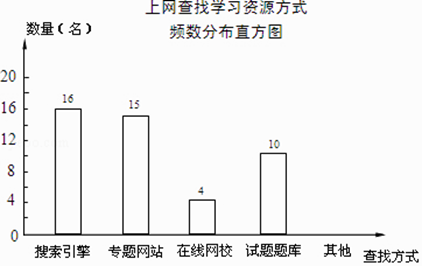
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?