题目内容
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
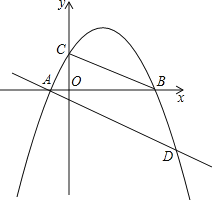
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
【答案】(1)、y=-![]() +
+![]() x+2;(2)、E点坐标为(0,2),(3,2).
x+2;(2)、E点坐标为(0,2),(3,2).
【解析】
试题分析:(1)、首先设出函数的解析式,然后利用待定系数法进行求解;(2)、首先根据题意判定△ABE只能是以点E为直角顶点的三角形,然后求出BC的长度,根据三角形相似求出点E的坐标.
试题解析:(1)、∵抛物线经过点C(0,2) ∴设该抛物线的解析式为y=a![]() +bx+2
+bx+2
将A、B两点坐标代入解析式得:![]() 解得:
解得:
∴抛物线的解析式为:y=-![]() +
+![]() x+2
x+2
(2)、存在
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能是以点E为直角顶点的三角形.
在Rt△BOC中,OC=2,OB=4, ∴BC=![]() =
=![]() .
.
在Rt△BOC中,设BC边上的高为h,则![]() ×
×![]() h=
h=![]() ×2×4, ∴h=
×2×4, ∴h=![]() .
.
∵△BEA∽△COB,设E点坐标为(x,y), ∴![]() =
=![]() ,∴y=±2
,∴y=±2
将y=2代入抛物线y=-![]() +
+![]() x+2,得
x+2,得![]() =0,
=0,![]() =3.
=3.
当y=﹣2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).


练习册系列答案
相关题目