题目内容
【题目】如图，∠MON=90°，点A、B分别在直线OM、ON上，BC是∠ABN的平分线.
（1）如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题：
①当∠ABO＝30°时，∠ADB＝ °
②当点A、B分别在射线OM、ON上运动时（不与点O重合），试问:随着点A、B的运动，∠ADB的大小会变吗？如果不会，请求出∠ADB的度数；如果会，请求出∠ADB的度数的变化范围；
（2）如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠，使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
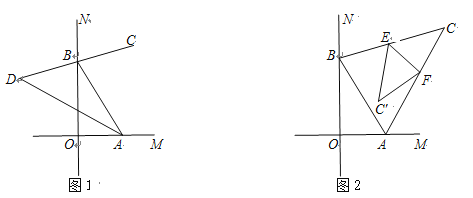
【答案】（1）①45；②∠ADB的大小不会变，为45°；
（2）∠BEC′+∠AFC′ 的度数是90°；
【解析】试题分析: (1) ①根据角平分线的定义可得: ∠NBC=∠ABC,然后根据对顶角相等可得: ∠NBC=∠DBO,然后由已知可得: ∠ABO＝30°，然后由三角形外角的性质可得: ∠NBA=∠BOA+∠BAO =120°,进而可得: ∠NBC=∠ABC=60°,然后由AD是∠OAB的平分线得到∠BAD=
∠BAO=15°,最后由∠BAD+∠BDA=∠ABC即可求出答案;
②∠ADB的大小不随点A,B的移动而发生变化,根据三角形的一个外角等于和它不相邻的两个内角的和, ∠ABN=∠OAB+∠MON, ∠CBA=∠ADB+∠DAB,再根据角平分线的定义∠DAB=
∠OAB, ∠CBA=
∠ABN,代入整理即可得到∠ADB=
∠MON=45°.
(2)首先根据已知证出∠C＝45°，从而得到∠C EC′+∠CFC′＝2(180°-∠C)=270°，进而得到∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°。
试题解析:
（1）①45
②设∠ABO＝α，
∵∠MON＝90°
∴∠BAD＝
,∠ABC＝
∴∠ABD＝180°-∠ABC=
∴∠ADB＝180°-∠BAD -∠ABD=45°
（2）∵∠MON＝90°
∴∠ABO+∠BAO＝90°
∴∠CAB+∠CBA＝
(∠BAM+∠ABN)=135°
∴∠C＝45°
∴∠C EC′+∠CFC′＝2(180°-∠C)=270°
∴∠BEC′+∠AFC′=360°-(∠C EC′+∠CFC′)=90°
