题目内容
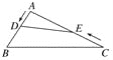
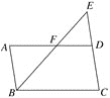
【题目】如图，四边形ABCD是平行四边形，E为边CD延长线上一点，连接BE交边AD于点F.请找出一对相似三角形，并加以证明．
【答案】见解析.
【解析】
选择△ABF∽△DEF，根据四边形ABCD是平行四边形可知AB∥CD，再由平行线的性质得出∠ABF＝∠E，∠A＝∠FDE，据此可得出结论．
解 ①选择：△ABF∽△DEF
理由：∵四边形ABCD是平行四边形，
∴AB∥CD.
∴∠ABF＝∠E，∠A＝∠FDE，
∴△ABF∽△DEF.
②选择：△EDF∽△ECB
理由：∵四边形ABCD是平行四边形，
∴AD∥BC.
∴∠C＝∠FDE.
又∵∠E＝∠E，
∴△EDF∽△ECB.
③选择：△ABF∽△CEB
理由：∵四边形ABCD是平行四边形，
∴AB∥CD，∠A＝∠C.
∴∠ABF＝∠E.
∴△ABF∽△CEB.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
