题目内容
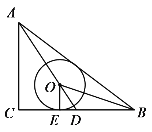
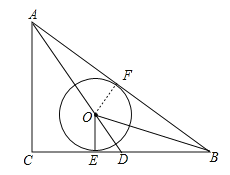
【题目】如图,![]() ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
ABC中,∠C=90°,AC=6,AB=10,点O在BC边的中线AD上,OB 平分∠ABC,⊙O与BC相切于点E.
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)作OF垂直AB于点F,然后根据角平分线的性质定理即可证得OE=OF,从而证得结论;
(2)根据勾股定理求得BC,进而求得CD=DB=2,设⊙O的半径为r,然后根据S△ACD+S△COB+S△AOB=S△ABC,得到![]() ACCD+
ACCD+![]() BDr+
BDr+![]() ACBC,解关于r的方程即可求得半径;
ACBC,解关于r的方程即可求得半径;
(3)证得Rt△ODE∽Rt△ADC,根据相似三角形的性质求得DE=![]() ,即可求得BF=BE=
,即可求得BF=BE=![]() ,AF=AB-BF=
,AF=AB-BF=![]() ,解直角三角形即可求得
,解直角三角形即可求得![]() .
.
解:(1)证明:如图,作OF⊥AB于点F,
∵⊙O与BC相切于点E,
∴OE⊥BC
又∵OB 平分∠ABC
∴OE=OF,
∴AB为⊙O的切线
(2)∵∠C=90°,AC=6,AB=10,
∴由勾股定理得BC=8,
又D为BC的中点,
∴CD=DB=4,
设⊙O的半径为r,
∵S△ACD+S△BOD+S△AOB=S△ABC
∴12+2r+5r=24 ,解得r=![]()
∴⊙O的半径为![]()
(3)解:∵∠C=90°,OE⊥BC,
∴OE∥AC,
∴Rt△ODE∽Rt△ADC,
∴![]() ,
,
∴DE=![]() ,
,
又OE=OF,OB=OB
∴Rt△BOE≌Rt△BOF
∴BF=BE=![]() ,
,
∴AF=AB﹣BF=![]()
∴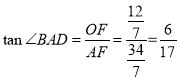 ./span>
./span>

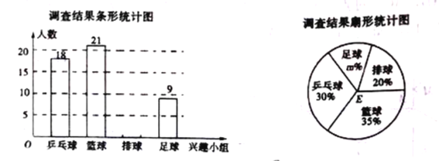
【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.