题目内容
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.

【答案】(1)二次函数的关系式为![]() ;(2)①
;(2)①![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() ;②见解析
;②见解析
【解析】
(1)利用待定系数法即可得到答案;
(2)①设![]() ,由点的对称性得到
,由点的对称性得到![]() ,再由勾股定理得到答案;②设直线
,再由勾股定理得到答案;②设直线![]() 与x轴交于点D,求得直线
与x轴交于点D,求得直线![]() 解析式,再结合题意即可得到答案.
解析式,再结合题意即可得到答案.
解:(1)∵二次函数顶点为![]()
∴设顶点式![]()
∵二次函数图象过点![]()
∴![]() ,解得:
,解得:![]()
∴二次函数的关系式为![]()
(2)设![]()
∴直线![]() 解析式为:
解析式为:![]()
∵![]() 交对称轴l于点M
交对称轴l于点M
∴当![]() 时,
时,![]()
∴![]()
∵点M、N关于点P对称
∴![]() ,
,
∴![]() ,即
,即![]()
①∵![]()
∴![]()
∴![]()
解得:![]()
∴![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,B
,B![]()
∴![]() ,
,![]()
∴![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() .
.
②证明:如图,设直线![]() 与x轴交于点D
与x轴交于点D
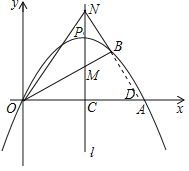
∵![]() 、
、![]()
设直线![]() 解析式为
解析式为![]()
∴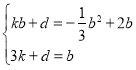 解得:
解得: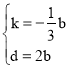
∴直线![]() :
:![]()
当![]() 时,
时,![]() ,解得:
,解得:![]()
∴![]()
∵![]() ,
,![]() 轴
轴
∴![]() 垂直平分
垂直平分![]()
∴![]()
∴![]()

练习册系列答案
相关题目