Question

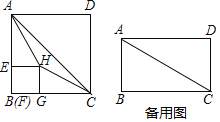
【题目】在矩形中，连结，点E从点B出发，以每秒1个单位的速度沿着的路径运动，运动时间为t（秒）．过点E作于点F，在矩形的内部作正方形．

（1）如图，当时，

①若点H在的内部，连结、，求证：；

②当时，设正方形与的重叠部分面积为S，求S与t的函数关系式；

（2）当，时，若直线将矩形的面积分成1︰3两部分，求t的值．

Answer 1

【答案】（1）①证明见解析；②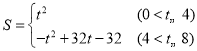；（3）t的值为或或．

【解析】

（1）①如图1中，证明即可解决问题．

②分两种情形分别求解：如图1中，当时，重叠部分是正方形．如图2中，当时，重叠部分是五边形．

（2）分三种情形分别求解：①如图3﹣1中，延长交于M，当时，直线将矩形的面积分成1︰3两部分．②如图3﹣2中，延长交于M交的延长线于K，当时，直线将矩形的面积分成1︰3两部分．③如图3﹣3中，当点E在线段上时，延长交于M，交的延长线于N．当时，直线将矩形的面积分成1︰3两部分．

解：（1）①如图1中，

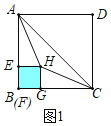
∵四边形是正方形，，

∴，，，

∴，

∵，

∴，

∴．

②如图1中，当时，重叠部分是正方形，．

如图2中，当时，重叠部分是五边形，．

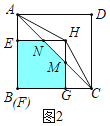
综上所述，．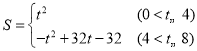

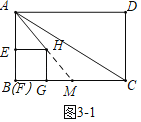
（2）如图3﹣1中，延长交于M，当时，直线将矩形的面积分成1︰3两部分．

∵，

∴，

∴，

∴．

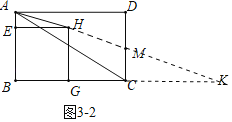
如图3﹣2中，延长交于M交的延长线于K，当时，直线将矩形的面积分成1︰3两部分，易证，

∵，

∴，

∴，

∴．

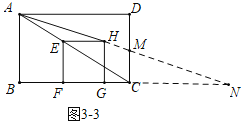
如图3﹣3中，当点E在线段上时，延长交于M，交的延长线于N．当时，直线将矩形的面积分成1︰3两部分，易证．

在中，，

∵，

∴，

∴，

∴，

∵，

∴，

∴，

解得．

综上所述，满足条件的t的值为或或．