题目内容
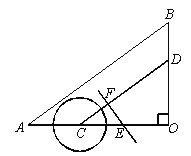
【题目】如图,草原上,一牧童在A处放马,牧童家在B处,A、B处距河岸的距离AC,BD的长分别为500m和700m,且CD=500m,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,牧童将马牵到河边什么地方饮水,才能使走过的路程最短？牧童最少要走多少m?
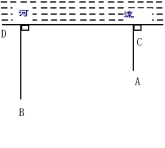
【答案】AE为牧童要走的最短路程；1300米
【解析】
试题分析：首先作点B关于CD的对称点E，根据对称的性质得出△MDE≌△MDB，从而得出AE为牧童要走的最短路程，然后根据Rt△ANE的勾股定理得出答案.
试题解析：
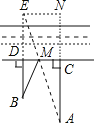
点B关于CD的对称点E， 由对称的性质可知，BD=ED，∠EDM=∠MDB，DM=DM， ∴△MDE≌△MDB，
∴BM=ME，BM+AM=ME+AM=AE，即AE为牧童要走的最短路程．
∵EN=CD=500米，AN=NC+AC=700+500=1200米，
∴在Rt△ANE中，AE=
=1300米．
故牧童至少要走1300米．
练习册系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克） |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）20筐白菜中，最重的一筐比最轻的一筐重______千克；
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价
元，则出售这20筐白菜可卖多少元？
