题目内容
【题目】如图,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H. 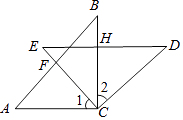
(1)求证:CF=CH;
(2)△ABC不动,将△EDC绕点C旋转到∠BCE=45°,证明:四边形ACDM是菱形.
【答案】
(1)证明:在△ACB和△ECD中,
∵∠ACB=∠ECD=90°,
∴∠1+∠ECB=∠2+∠ECB,
∴∠1=∠2;
又∵AC=CE=CB=CD,
∴∠A=∠D=45°;
在△CFA和△CHD中,
∵ 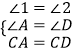 ,
,
∴△CFA≌△CHD(AAS),
∴CF=CH
(2)证明:∵∠ACB=∠ECD=90°,∠BCE=45°,
∴∠1=45°,∠2=45°.
又∵∠E=∠B=45°,
∴∠1=∠E,∠2=∠B,
∴AC∥MD,CD∥AM,
∴四边形ACDM是平行四边形,
又∵AC=CD,
∴平行四边形ACDM是菱形
【解析】(1)先根据直角三角形的性质得出∠1=∠2,再由AAS定理得出△CFA≌△CHD,进而可得出结论;(2)根据∠BCE=45°得出∠1=∠2=45°.根据∠E=∠B=45°得出∠1=∠E,∠2=∠B,故可得出四边形ACDM是平行四边形,再由AC=CD即可得出结论.
【考点精析】本题主要考查了菱形的判定方法和旋转的性质的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

练习册系列答案
相关题目