题目内容
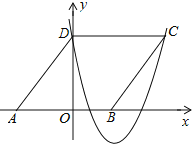
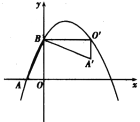
【题目】如图,抛物线y=![]() 与x轴、y轴交于A、B两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B,点O落到点O′的位置,点A落到点A′的位置.
与x轴、y轴交于A、B两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B,点O落到点O′的位置,点A落到点A′的位置.
(1)求点O′和点A′的坐标;
(2)将抛物线沿y轴方向平移后经过点A′,求平移后所得抛物线对应的函数关系式;
(3)设(2)中平移后所得抛物线与y轴的交点为C,与x轴的交点为D,点M在x轴上,点N在平移后所得抛物线上,求出以点C、D、M、N为顶点的四边形是以CD为边的平行四边形时点N的坐标.
【答案】(1)O′(2,2),A′(2,1);(2)![]() ;(3)(2,1),(3,-1)和(-1,-1).
;(3)(2,1),(3,-1)和(-1,-1).
【解析】
(1)先求出抛物线与x轴和y轴的交点A(-1,0),B(0,2),再利用旋转的性质得BO′=BO=2,O′A′=OA=1,∠OBO′=90°,∠BO′A′=∠BOA=90°,然后利用第一象限点的坐标特征写出点O′和点A′的坐标;
(2)先判断点O′在抛物线![]() 上,利用抛物线沿y轴方向平移后经过点A′得到把抛物线
上,利用抛物线沿y轴方向平移后经过点A′得到把抛物线![]() 向下平移1个单位,然后利用抛物线的平移规律写出平移后的抛物线解析式;
向下平移1个单位,然后利用抛物线的平移规律写出平移后的抛物线解析式;
(3)先确定C(0,1),利用平行四边形的性质得CD∥MN,讨论:当N点在x轴上方的抛物线上时,CN∥DM,此时N点的纵坐标为1,N点与A′点重合,N点坐标为(2,1);当N点在x轴下方的抛物线上时,DN∥CM,则点C和点N到x轴的距离相等,N点的纵坐标为-1,则解方程![]() 得此时N点坐标.
得此时N点坐标.
解析(1)当y=0时,![]() ,解得x=-1,x=3,则A(-1,0),
,解得x=-1,x=3,则A(-1,0),
当x=0时,y=2,则B(0,2),
∵△OAB绕点B逆时针旋转90°后得到△O′A′B.
∴BO′=BO=2,O′A′=OA=1,∠OBO′=90°,∠BO′A′=∠BOA= 90°,
∴O′(2,2),A′(2,1).
(2)∵当x=2时,![]() ,
,
∴点O′在抛物线![]() 上,
上,
∵抛物线沿y轴方向平移后经过点A′,
∴把抛物线![]() 向下平移1个单位,
向下平移1个单位,
∴平移后的抛物线解析式为![]() .
.
(3)当x=0时,![]() ,则C(0,1),
,则C(0,1),
∵以点C、D、M、N为顶点的四边形是以CD为边的平行四边形.
∴CD//MN,
当N点在x轴上方的抛物线上时,CN//DM,
此时N点的纵坐标为1,N点与A′点重合,N点坐标为(2,1);
当N点在x轴下方的抛物线上时,DN∥CM,则点C和点N到x轴的距离相等,则N点的纵坐标为-1,
当y=-1时,![]() ,解得x=3,x=-1,
,解得x=3,x=-1,
此时N点坐标为(3,-1)或(-1,-1).
综上所述,满足条件的N点坐标有(2,1),(3,-1)和(-1,-1).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案