题目内容
【题目】如图,AB是⊙O的弦,AB=4,过圆心O的直线垂直AB于点D,交⊙O于点C和点E,连接AC、BC、OB,cos∠ACB= ![]() ,延长OE到点F,使EF=2OE.
,延长OE到点F,使EF=2OE. 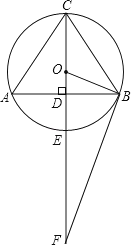
(1)求⊙O的半径;
(2)求证:BF是⊙O的切线.
【答案】
(1)
解:连OA,如图,
∵直径CE⊥AB,
∴AD=BD=2,弧AE=弧BE,
∴∠ACE=∠BCE,∠AOE=∠BOE,
又∵∠AOB=2∠ACB,
∴∠BOE=∠ACB,
而cos∠ACB= ![]() ,
,
∴cos∠BOD= ![]() ,
,
在Rt△BOD中,设OD=x,则OB=3x,
∵OD2+BD2=OB2,
∴x2+22=(3x)2,解得x= ![]() ,
,
∴OB=3x= ![]() ,
,
即⊙O的半径为 ![]() ;
;
(2)
证明:∵FE=2OE,
∴OF=3OE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
而 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
而∠BOF=∠DOB,
∴△OBF∽△ODB,
∴∠OBF=∠ODB=90°,
∵OB是半径,
∴BF是⊙O的切线.
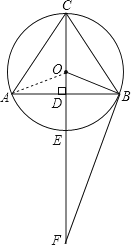
【解析】(1)连OA,由直径CE⊥AB,根据垂径定理可得到AD=BD=2,弧AE=弧BE,利用圆周角定理得到∠ACE=∠BCE,∠AOB=2∠ACB,且∠AOE=∠BOE,则∠BOE=∠ACB,可得到cos∠BOD=cos∠ACB= ![]() ,在Rt△BOD中,设OD=x,则OB=3x,利用勾股定理可计算出x=
,在Rt△BOD中,设OD=x,则OB=3x,利用勾股定理可计算出x= ![]() ,则OB=3x=
,则OB=3x= ![]() ;(2)由于FE=2OE,则OF=3OE=
;(2)由于FE=2OE,则OF=3OE= ![]() ,则
,则 ![]() =
= ![]() ,而
,而 ![]() =
= ![]() ,于是得到
,于是得到 ![]() =
= ![]() ,根据相似三角形的判定即可得到△OBF∽△ODB,根据相似三角形的性质有∠OBF=∠ODB=90°,然后根据切线的判定定理即可得到结论.
,根据相似三角形的判定即可得到△OBF∽△ODB,根据相似三角形的性质有∠OBF=∠ODB=90°,然后根据切线的判定定理即可得到结论.

【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元