题目内容
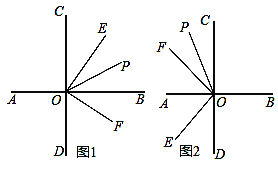
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.
【答案】(1)①∠BOF= 30°,∠POE=30°,②∠POE=∠BOP(2)①∠POE=∠BOP②∠POE+∠DOP=270°
【解析】
(1)①根据余角的性质得到∠BOF=∠COE=30°,求得∠COF=90°+30°=120°,根据角平分线的定义即可得到结论;
②根据垂线的性质和角平分线的定义即可得到结论;
(2)①根据角平分线的定义得到∠COP=∠POF,求得∠POE=90°+∠POF,∠BOP=90°+∠COP,于是得到∠POE=∠BOP;
②根据周角的定义即可得到结论.
(1)①∵CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE=30°,
∴∠COF=90°+30°=120°,
∵OP平分∠COF,
∴∠COP=![]() ∠COF=60°,
∠COF=60°,
∴∠POE=∠COP﹣∠COE=30°;
②CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE,
∵OP平分∠COF,
∴∠COP=∠POF,
∴∠POE=∠COP﹣∠COE,∠BOP=∠POF﹣∠BOF,
∴∠POE=∠BOP;
(2)①∵∠EOF=∠BOC=90°,
∵PO平分∠COF,
∴∠COP=∠POF,
∴∠POE=90°+∠POF,∠BOP=90°+∠COP,
∴∠POE=∠BOP;
②∵∠POE=∠BOP,∠DOP+∠BOP=270°,
∴∠POE+∠DOP=270°.