题目内容
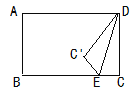
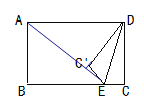
【题目】如图，矩形ABCD中，CD=6，E为BC边上一点，且EC=2将△DEC沿DE折叠，点C落在点C'．若折叠后点A，C'，E恰好在同一直线上，则AD的长为（ ）
A.8B.9C.
D.10
【答案】D
【解析】
在Rt△DEC中，由勾股定理可得DE的长．设AD=x，则BE=x-2，AB=DC=C'D．
由Rt△AC'D≌△EBA，得到BE=AC'=x-2．在Rt△AC'D中，由勾股定理即可得出结论．
解：如图，由勾股定理得：DE=
．
设AD=x，则BE=x-2，AB=DC=C'D．
∵AD∥BE，∴∠DAE=∠AEB，∴Rt△AC'D≌△EBA（AAS），∴BE=AC'=x-2．
在Rt△AC'D中，由勾股定理得：AD2=AC'2+C'D2，即x2=（x-2）2+62，解得：x=10，即AD=10．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】如图，一次函数y＝x＋m的图象与反比例函数y＝
的图象交于A，B两点，且与x轴交于点C，点A的坐标为(2，1)．
(1)求m及k的值；
(2)求点C的坐标，并结合图象写出不等式组0＜x＋m≤
的解集．
【题目】（本题有两道题，请从（1）、（2）题中选一题作答即可）
（1）某品牌太阳镜由一个镜架和两个镜片配套构成，每个工人每天可以加工
个镜架或者加工
个镜片，现有
名工人，应怎么安排人力，才能使每天生产的镜架和镜片配套？能做成多少副太阳镜？
（2）去年春季，蔬菜种植场在
公顷的大棚地里分别种植了茄子和西红柿，总费用是
万元.其中，种植茄子和西红柿每公顷的费用和每公顷获利情况如表：
每公顷费用 万元 | 每公顷获利 万元 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题：
①求出茄子和西红柿的种植面积各为多少公顷？
②种植场在这一季共获利多少万元？
