题目内容
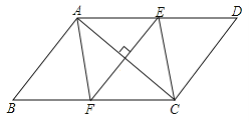
【题目】如图①,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:DEBF=EF;
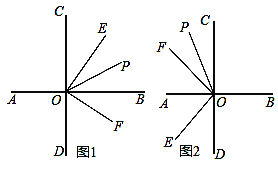
(2)若点G为CB延长线上一点,其余条件不变。请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明);

【答案】(1)见解析(2)DE+BF=EF
【解析】
(1)本题的关键是求三角形ADE和BAF全等,以此来得出DE=AF=AE+EF=BE+EF,这两个三角形中已知的条件有AD=BA,一组直角,关键是再找出一组对应角相等,可通过证明∠DAF和∠ABF来实现.(通过平行和等角的余角相等来证得)
(2)方法同(1)还是正三角形ADE和BAF全等,得出DE=AF,BF=AE,只不过本题的结论是DE+BF=EF
(1)证明:∵四边形ABCD是正方形,BF⊥AG,
DE⊥AG,
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°
∴∠BAF=∠ADE
∴△ABF≌△DAE
∴BF=AE, AF=DE
∴DE-BF=AF-AE=EF
(2)如图,DE+BF=EF

练习册系列答案
相关题目