Question

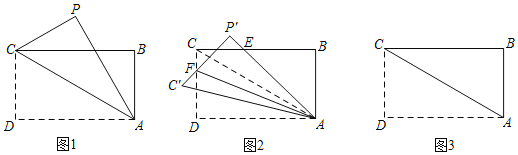
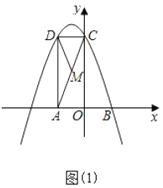
【题目】已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B(点A在点B左侧)，根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．

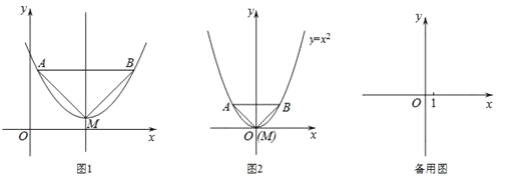
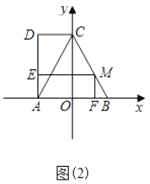
（1）①如图2,求出抛物线y=x2的“完美三角形”斜边AB的长；

②请写出一个抛物线的解析式，使它的完美三角形与y=x2+1的“完美三角形”全等；

（2）若抛物线y=ax2+4的“完美三角形”的斜边长为4，求a的值；

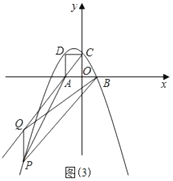
（3）若抛物线y=mx2+2x+n5的“完美三角形”斜边长为n,且y=mx2+2x+n5的最大值为1，求m，n的值．

Answer 1

【答案】（1）①2；②；（2）a＝；（3）， ．

【解析】

（1）①过点B作BN⊥x轴于N，根据△AMB为等腰直角三角形，AB∥x轴，所以∠BMN＝∠ABM＝45，所以∠BMN＝∠MBN，得到MN＝BN，设B点坐标为（n，n），代入抛物线y＝x2，得n＝n2，解得n＝1，n＝0（舍去），所以B（1，1），求出BM的长度，利用勾股定理，即可解答；

②因为抛物线y＝x2＋2与y＝x2+1的形状相同，所以抛物线y＝x2＋2与y＝x2+1的“完美三角形”的边长的数量关系是相等的，故可写出；

（2）根据抛物线y＝ax2与抛物线y＝ax2＋4的形状相同，所以抛物线y＝ax2与抛物线y＝ax2＋4的“完美三角形”全等，由抛物线y＝ax2＋4的“完美三角形”斜边的长为4，可得抛物线y＝ax2的“完美三角形”斜边的长为4，从而确定B点坐标为（2，2）或（2，2），把点B代入y＝ax2中，即可求出a的值；

（3）根据y＝mx2＋2x＋n5的最大值为1，得到＝1，化简得mn4m1＝0，抛物线y＝mx2＋2x＋n5的“完美三角形”斜边长为n，所以抛物线y＝mx2的“完美三角形”斜边长为n，所以B点坐标为(，)，代入抛物线y＝mx2，得mn＝2，即可求出m,n的值．

（1）①过点B作BN⊥x轴于N，如图2，

∵△AMB为等腰直角三角形，

∴∠ABM=45 ，

∵AB∥x轴，

∴∠BMN=∠ABM=45 ，

∴∠MBN=9045=45 ，

∴∠BMN=∠MBN，

∴MN=BN，

设B点坐标为(n,n),代入抛物线y=x2 ，

得n=n2，

∴n=1,n=0(舍去)，

∴B(1,1)

∴MN=BN=1，

∴MB=

∴MA=MB=

在Rt△AMB中,AB=,

∴抛物线y=x2的“完美三角形”的斜边AB=2；

②∵抛物线y＝x2＋2与y=x2+1的形状相同，

∴抛物线y＝x2＋2与y=x2+1的“完美三角形”的边长的数量关系是相等的，

故可写出抛物线：y=x2+2；

（2）解：∵抛物线y=ax2与抛物线y=ax2+4的形状相同，

∴抛物线y=ax2与抛物线y=ax2+4的“完美三角形”全等，

∵抛物线y=ax2+4的“完美三角形”斜边的长为4，

∴抛物线y=ax2的“完美三角形”斜边的长为4，

∴B点坐标为(2,2)或(2,2)，

把点B代入y=ax2中，得a=±；

（3）解：∵y=mx2+2x+n5的最大值为1，

∴ =1，

∴mn4m1=0，

∵抛物线y=mx2+2x+n5的“完美三角形”斜边长为n，

∴抛物线y=mx2的“完美三角形”斜边长为n，

∴B点坐标为(，－)，

∴代入抛物线y=mx2，得()2×m= ，

∴mn=2或n=0(不合题意舍去)，

代入mn4m1=0，解得m=，

∴n=．