题目内容
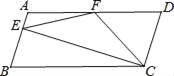
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A.![]() =
=![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
【答案】A.
【解析】
试题分析:已知∠B=∠C=36°,可得AB=AC,∠BAC=108°,又因DH垂直平分AB,EG垂直平分AC,根据中垂线性质得DB=DA,EA=EC,所以∠B=∠DAB=∠C=∠CAE=36°,即可判定△BDA∽△BAC,根据相似三角形的性质可得![]() =
=![]() ,再由∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,所以∠ADC=∠DAC,即可得CD=CA=BA,即BD=BC﹣CD=BC﹣AB,所以
,再由∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC﹣∠BAD=72°,所以∠ADC=∠DAC,即可得CD=CA=BA,即BD=BC﹣CD=BC﹣AB,所以![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,选项A错误;因为∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,所以∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,即可得AD,AE将∠BAC三等分,选项B正确;因为∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,可得∠BAE=∠CAD,在△BAE和△CAD中,
,选项A错误;因为∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,所以∠DAE=∠BAC﹣∠DAB﹣∠CAE=36°,即∠DAB=∠DAE=∠CAE=36°,即可得AD,AE将∠BAC三等分,选项B正确;因为∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,可得∠BAE=∠CAD,在△BAE和△CAD中, ,所以△BAE≌△CAD,选项C正确;由△BAE≌△CAD可得S△BAE=S△CAD,S△BAD+S△ADE=S△CAE+S△ADE,所以S△BAD=S△CAE,又因DH垂直平分AB,EG垂直平分AC,所以S△ADH=
,所以△BAE≌△CAD,选项C正确;由△BAE≌△CAD可得S△BAE=S△CAD,S△BAD+S△ADE=S△CAE+S△ADE,所以S△BAD=S△CAE,又因DH垂直平分AB,EG垂直平分AC,所以S△ADH=![]() S△ABD,S△CEG=
S△ABD,S△CEG=![]() S△CAE,即S△ADH=S△CEG,选项D正确.故答案选A.
S△CAE,即S△ADH=S△CEG,选项D正确.故答案选A.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目