��Ŀ����
����Ŀ����1����ͼ1��ʾ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O������գ�![]() = ��ֱ��д���𰸣���
= ��ֱ��д���𰸣���
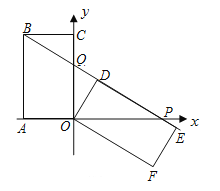
��2����ͼ2��ʾ������1���е���BOC�Ƶ�B��ʱ����ת�õ���BO1C1������AO1��DC1����������߶�AO1��DC1֮���������ϵ����֤��֮��
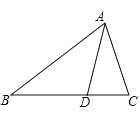
��3����ͼ3��ʾ������ABCD��Rt��BEF�й�������B������BEF=90������EBF=��ABD=30������![]() ��ֵ�Ƿ�Ϊ��ֵ�����Ƕ�ֵ���������ֵ�������Ƕ�ֵ�����������.
��ֵ�Ƿ�Ϊ��ֵ�����Ƕ�ֵ���������ֵ�������Ƕ�ֵ�����������.

���𰸡���1��![]() ����2��
����2��![]() ��3��
��3��![]()
![]()
��������
�����������1�����������ε����ʺ͵���ֱ�������ε����ʼ��㼴�ɣ�
��2��������ת�任�����ʵõ���ABO=��O1B��C1�����������ε����ʵõ�![]() ��֤����ABO1�ס�DBC1���������������ε����ʽ��
��֤����ABO1�ס�DBC1���������������ε����ʽ��
��3���������ҵĶ���;��ε�����֤����AEB�ס�DFB���������������ε����ʼ��㼴��.
�����������1�����ı���ABCD�������Σ�
��AD=DC����AOD�ǵ���ֱ�������Σ�
��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���ߡ�BOC�Ƶ�B��ʱ����ת�õ���BO1C1��
���ABO=��O1B��C1��
���ABO1=��DBC1��
���ı���ABCD�������Σ�
��![]() ����
����![]() ��
��
��![]() ������ABO1=��DBC1��
������ABO1=��DBC1��
���ABO1�ס�DBC1��
��![]() ��
��
��3����Rt��EBF����EBF=30����
��![]() =
=![]() ��
��
��Rt��ABD����ABD=30����
��![]() ��
��
��![]() ��
��
�ߡ�EBF=��ABD��
���EBA=��FBD��
���AEB�ס�DFB��
��![]() .
.