题目内容
将两块含30°角且大小相同的直角三角板如图1摆放.
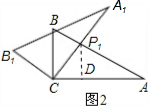
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,求证:CP1=
AP1;
(2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3),点P2是A2C与AB的交点.线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4),连接P3P2,求证:P3P2⊥AB.

(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,求证:CP1=
| ||
| 2 |
(2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3),点P2是A2C与AB的交点.线段CP1与P1P2之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
(3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4),连接P3P2,求证:P3P2⊥AB.
(1)证明:过点P1作CA的垂线,垂足为D.
易知:△CDP1为等腰直角三角形,
△P1DA是直角三角形,且∠A=30°,
所以CP1=
P1D,P1D=
AP1,
故CP1=
AP1.
(2)过点P1作CA2的垂线,垂足为E,
易知:△P1EP2是等腰直角三角形,
(其中∠2=∠A+∠P2CA=45°),
因为△P1CE是直角三角形,且∠1=30°,
所以CP1=2P1E,P1E=
P1P2,
故CP1=
P1P2.
(3)证明:将图3中线段CP1绕点C顺时针旋转60°到CP3,
易证:△CP1P2≌△CP3P2,于是∠CP3P2=∠CP1P2=105°,
∴∠P1P2P3=360°-105°×2-60°=90°,
故P2P3⊥AB.
易知:△CDP1为等腰直角三角形,
△P1DA是直角三角形,且∠A=30°,
所以CP1=
| 2 |
| 1 |
| 2 |
故CP1=
| ||
| 2 |
(2)过点P1作CA2的垂线,垂足为E,

易知:△P1EP2是等腰直角三角形,
(其中∠2=∠A+∠P2CA=45°),
因为△P1CE是直角三角形,且∠1=30°,
所以CP1=2P1E,P1E=
| ||
| 2 |
故CP1=
| 2 |
(3)证明:将图3中线段CP1绕点C顺时针旋转60°到CP3,
易证:△CP1P2≌△CP3P2,于是∠CP3P2=∠CP1P2=105°,
∴∠P1P2P3=360°-105°×2-60°=90°,
故P2P3⊥AB.


练习册系列答案
相关题目







